Matematiksel yaklaşım ile Evrişim işlemi

Evrişim (Convolution) işlemi sinyal ve görüntü işleme için önemli bir işlemdir. Yazıya ilk olarak evrişim(convolution) işleminin formülü vererek başlayalım. Daha sonra bu formülün bize ne anlatmaya çalıştığına da değineceğiz.

$f(x)g(x)= \int_{-\infty }^{\infty }{f(\tau )g(x-\tau )d\tau }$

Bu formülde f(x) input (girdi), g(x) ise impulse response (dürtü yanıtı). * işareti ise Convolution (Evrişim) işlemini belirtmektedir. Evrişim işlemini anlamak, dürtü sinyaline ve sinyalimizi dürtü sinyalleri şeklinde yazabilmemize bağlıdır. Nasıl yani? İşler çok daha karışmadan sinyalimizi nasıl dürtü sinyalleri şeklinde yazabileceğimize bakalım.

1. Dürtü Sinyali (Impulse Fonksiyonu)

Peki dürtü sinyali nedir? Aşağıdaki şekilde gösterildiği gibi, sadece bir noktada uzunluğu 1 olan bir fonksiyondur.

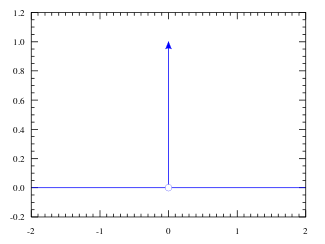
*Kaynak: https://en.wikipedia.org/wiki/Dirac_delta_function*

Matematiksel olarak:

$\delta (x-x_{0})=\bigg\{ \begin{gathered} 1,\quad x= x_{0} \\ 0,\quad x\neq x_{0} \\ \end{gathered}$

2. Sinyali ayrıştırma

Genel olarak sinyaller, daha sabit sinyallerin ağırlıklandırılmış hali ile ifade edilir. Örneğin Fourier serisinde, sinyaller kosinüs ve sinüs sinyalleri toplamı şeklinde yazılır. Biz bu işlemde kosinüs ve sinüs yerine ise sinyalimizi dürtü sinyalleri toplamı şeklinde yazacağız.

Aşağıdaki örnek ile devam edelim. Sinyalimiz şekildeki gibi olsun.

x[n]

Kaynak: http://www.songho.ca/dsp/convolution/convolution.html

Şimdi sinyali dürtü sinyalleri şeklinde yazmaya çalışalım. Dürtü sinyalinin n = 0 noktasında 1, diğer durumlarda hep 0 olduğunu hatırlayalım. x[0] noktası dürtü sinyalinin sadece iki katıdır. x[1] noktası dürtü sinyalinin bir birim sağa kaydırılıp 3 ile çarpılmasıyla oluşturabilir. x[2] noktasını ise dürtü sinyalini 2 birim sağa kaydırarak elde edebiliriz. Sonuç olarak aşağıdaki gibi yazabiliriz.

$x[0] = x[0].\delta [n-0]=2.\delta [n-0]\\ x[1] = x[1].\delta [n-1] = 3.\delta [n-1]\\ x[2] = x[2].\delta [n-2] = 1.\delta [n-2]\\ \\ x[n] = x[0].\delta[n]+x[1].\delta[n-1]+x[2].\delta[n-2]$

Daha da genelleştirirsek, herhangi bir sinyali aşağıdaki gibi dürtü sinyallerinden oluşacak şekilde yazabiliriz:

$x[n]=\sum_{k=-\infty}^{\infty}x[k]\delta[n-k]$

3. Dürtü Yanıtı (Impulse Response)

Dürtü yanıtı (Impulse Response), sisteme girdi olarak dürtü fonksiyonu verildiğinde sistemin verdiği çıktıdır. h[n] ile gösterilir.

$\delta[n] \rightarrow sistem \rightarrow h[n]$

Eğer sistem Time Invarient ise, yani zamandan bağımsız ise, belirli bir girdiye üretilen sonuç zamana bağlı olarak değişiklik göstermez.

$\delta[n-k] \rightarrow sistem \rightarrow h[n-k]$

Eğer sistem lineer ise, girdinin herhangi bir skalar bir sayıyla çarpımı çıktıyı da aynen etkiler.

$c.\delta[n] \rightarrow sistem \rightarrow c.h[n]$

Tanıma geri dönelim

Yukarıda bahsedilen özellikleri birleştirerek evrişim için formülü artık türetebiliriz. Lineer ve zamandan bağımsız (time invarient) sistemin cevabı, her bir girdinin etkisinin ayrı ayrı ele alınmasıyla bulunabilir. Yani:

$input \rightarrow x[n]= 2\delta[n]+3\delta[n-1] \\ output \rightarrow y[n]= 2h[n]+3h[n-1]$

Sistemin karakteristiği hakkında bilmemiz gereken en önemli şey, sistemin dürtü yanıtıdır. Eğer bunu bulabilirsek, sistemin herhangi bir sinyale karşı nasıl bir tepki vereceğini kolaylıkla bulabiliriz.

4. 2D Evrişim (Convolution)

Yukarıda verilen evrişim formülü 1D evrişimdir. Biz daha çok 2D evrişime değineceğiz. Fakat yine de 1D evrişim hakkında güzel bir örneği buraya bırakalım.

2D evrişim de aslında 1D evrişim sadece bir uzantısı diyebiliriz. Bu sefer, sadece tek bir eksende bu işlemi yapmak yerine iki eksende, x ve y ekseninde işlem yapacağız. 2D evrişim daha çok görüntü işleme uygulamalarında, görüntünün barındırdığı özellikleri bulmak için kullanılır.

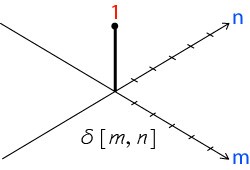
Dürtü (Impulse) fonksiyonu da 2 boyutlu uzayda da gösterilebilir. Yandaki şekilde bunun bir örneğini görmekteyiz. Dürtü fonksiyonunun değeri m ve n değerleri 0 iken 1, diğer durumlar için 0’dır. 2D dürtü fonksiyonu genelde kernel veya filtre olarak da adlandırılır.

Resim Kaynak: http://www.songho.ca/dsp/convolution/convolution.html

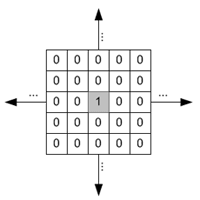
Bu resim ise dürtü fonksiyonunun 2D matris gösterimidir. Matriste 1 ile gösterilen yer merkez ve m = n = 0 noktasıdır.

Resim Kaynak: http://www.songho.ca/dsp/convolution/convolution.html

2D evrişim yukarıda verilen 1D evrişimde olduğu gibi ayrıştırılarak dürtü fonksiyonları ile yazılabilir. Tek fark bu sefer tek boyut yerine iki boyutta koordinat noktaları belirtiyoruz:

$x[m,n]=\sum_{j=-\infty}^{\infty}\sum_{i=-\infty}^{\infty}x[i,j].\delta[m-i,n-j]$

Lineer ve zamandan bağımsız bir sistemin çıktısı, $x[m,n]$ girdi sinyali ve $h[m,n]$ dürtü yanıtının (impulse response) evrişimi olarak ifade edilebilir. Lineer ve zamandan bağımsız bir sistem olan $y[m,n]$ , $x[m,n]$ ile $h[m,n]$ fonksiyonlarının evrişimi şeklinde yazılabilir.

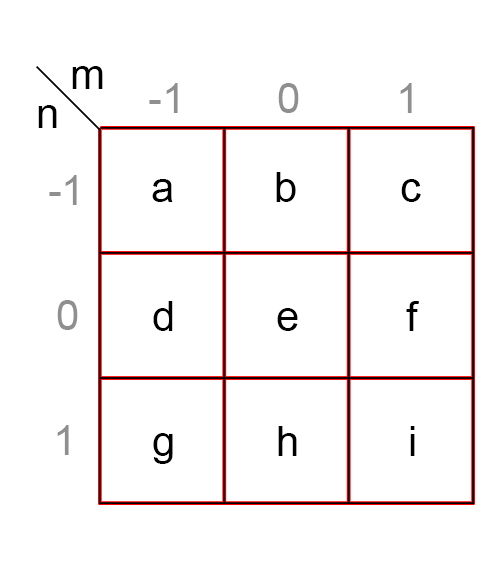
$y[m,n]=x[m,n]*h[m,n]=\sum_{j=-\infty}^{\infty}\sum_{i=-\infty}^{\infty}x[i,j].h[m-i,n-j]$

Filtre, 2D uzayda, merkezi orijinde olacak şekilde konumlanır. Yandaki resimden örnek verirsek, e noktası h[0,0] noktasında konumlanmıştır, a noktası ise h[-1,-1].

Şimdi rastgele bir nokta seçelim ve bu nokta için evrişimi hesaplayalım. Örnek olarak y(1,1) noktasındaki değeri hesaplayalım. Aşağıdaki verilen i ve j değerleri, filtrenin girdi üzerinde denk geldiği yerdeki konumlardır. Bu örnekte i değeri 0’dan 2’ye, j değeri de 0’dan 2’ye kadar değerler alacaktır.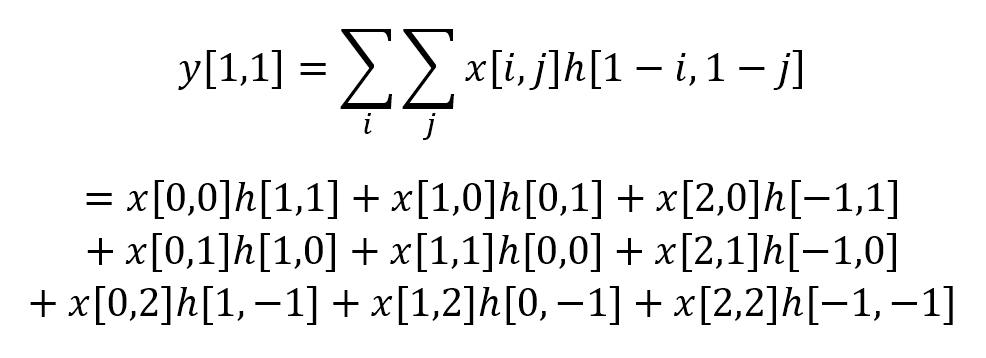

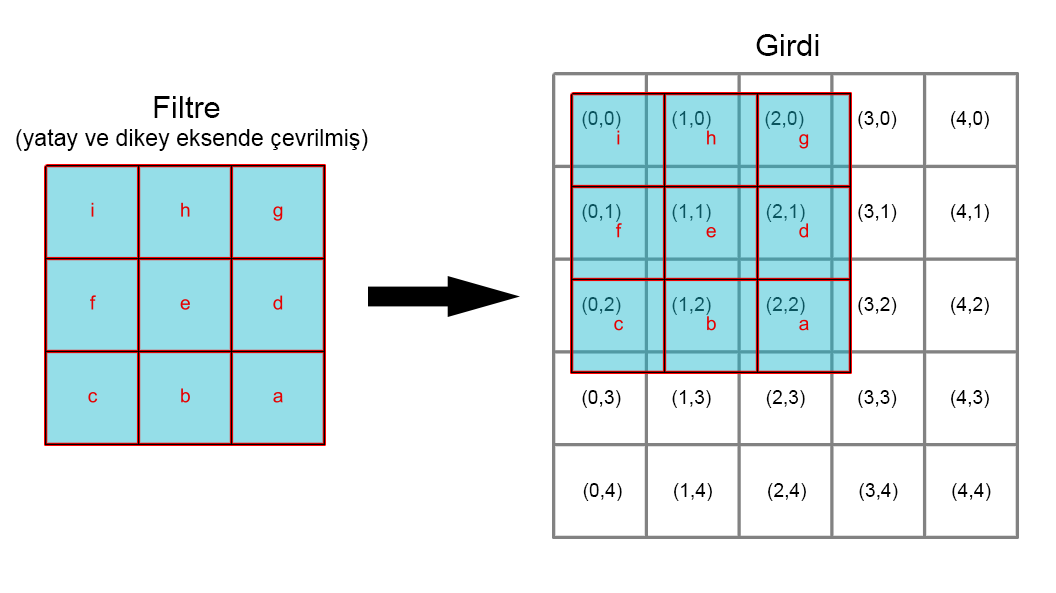
Burada dikkat edilmesi gereken şey, ilk başta tasarladığımız filtre hem yatayda hem de dikeyde ters dönerek işleme girmiştir.

Filtrenin yatayda ve dikeyde ters döndürmeden işleme almak için, birçok yapay sinir ağı kütüphanesi, çok benzer olan cross-correlation fonksiyonunu kullanmaktadır. Bu fonksiyonun evrişimden tek farkı, filtrenin döndürülmemesidir. Cross-correlation fonksiyonu aşağıda verilmiştir:

Filtremiz simetrik bir filtre olduğu zaman (Gaussian veya Laplacian gibi) korelasyon veya evrişim fonksiyonundan hangisini kullandığımız önemli değildir. Fakat simetrik olmayan bir filtre kullanıldığında bu durum oldukça önemli bir hale gelmektedir.

Evrişim işleminin birleşme özelliği vardır. Örnek vermek gerekirse resmimiz f‘yi önce g filtresi ile daha sonra h filtresi ile evrişim işlemine sokalım. f * g * h = f * (g * h) . Bu demek oluyor ki önce g ve h filtrelerini konvolüze ederek yeni bir filtre üretilip daha sonra resmimiz , sadece bu yeni üretilen filtre ile evrişim işlemine sokulabilir. Bu işlem g ve h filtrelerini birden fazla resim ile işleme sokmak istediğimiz zaman oldukça kullanışlıdır. Bir kere k = (g * h) işlemini tanımladıktan sonra her resmi k filtresinden geçirmemiz yeterli olacaktır. Cross-correlation işleminin ise birleşme özelliği yoktur.

Evrişim işleminde, koordinat parametreleri, filtrenin girdi üzerinde denk geldiği yere göre değişmekteydi. Çapraz korelasyon işleminde ise, filtremizin koordinatları i ve j değişkenleri olarak alınır. Yani yukarıdaki örnek için, evrişim işleminde i ve j değerleri 0’dan 2’ye kadar değişirken, çapraz korelasyon işleminde bu değerler -1’den 1’e kadar değişmektedir (filtremizin konumlandığı şekilde).

Cross-correlation işlemi template matching işlemlerinde oldukça elverişlidir. Fakat yukarıda bahsettiğimiz durumlar için birden fazla resimde birden fazla filtre kullanmak istersek evrişim işlemi çok daha verimli olabilmektedir.

Birçok yapay sinir ağı kütüphanesi, aslında evrişim işlemi yerine cross-correlation işlemini kullanmaktadır. Yani filtre, yatayda ve dikeyde döndürülmeden işleme girmektedir. Mesela TensorFlow, dokümantasyonunda bu durumu belirtmektedir.

Sonuç olarak, çapraz korelasyon işlemi, iki sinyalin birbirine olan benzerliklerini ayırt etmemizi sağlar. Evrişim işlemi ise bir sinyalin low-pass filtre gibi doğrusal ve zamanla değişmeyen bir sistemden nasıl etkilendiğini bulmamızı sağlar.